
Asia Pacific Academy of Science Pte. Ltd. (APACSCI) specializes in international journal publishing. APACSCI adopts the open access publishing model and provides an important communication bridge for academic groups whose interest fields include engineering, technology, medicine, computer, mathematics, agriculture and forestry, and environment.
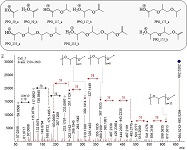
The (partial) replacement of synthetic polymers with bioplastics is due to increased production of conventional packaging plastics causing for severe environmental pollution with plastics waste. The bioplastics, however, represent complex mixtures of known and unknown (bio)polymers, fillers, plasticizers, stabilizers, flame retardant, pigments, antioxidants, hydrophobic polymers such as poly(lactic acid), polyethylene, polyesters, glycol, or poly(butylene succinate), and little is known of their chemical safety for both the environment and the human health. Polymerization reactions of bioplastics can produce no intentionally added chemicals to the bulk material, which could be toxic, as well. When polymers are used to food packing, then the latter chemicals could also migrate from the polymer to food. This fact compromises the safety for consumers, as well. The scarce data on chemical safety of bioplastics makes a gap in knowledge of their toxicity to humans and environment. Thus, development of exact analytical protocols for determining chemicals of bioplastics in environmental and food samples as well as packing polymers can only provide warrant for reliable conclusive evidence of their safety for both the human health and the environment. The task is compulsory according to legislation Directives valid to environmental protection, food control, and assessment of the risk to human health. The quantitative and structural determination of analytes is primary research task of analysis of polymers. The methods of mass spectrometry are fruitfully used for these purposes. Methodological development of exact analytical mass spectrometric tools for reliable structural analysis of bioplastics only guarantees their safety, efficacy, and quality to both humans and environment. This study, first, highlights innovative stochastic dynamics equations processing exactly mass spectrometric measurands and, thus, producing exact analyte quantification and 3D molecular and electronic structural analyses. There are determined synthetic polymers such as poly(ethylenglycol), poly(propylene glycol), and polyisoprene as well as biopolymers in bags for foodstuffs made from renewable cellulose and starch, and containing, in total within the 20,416–17,495 chemicals per sample of the composite biopolymers. Advantages of complementary employment in mass spectrometric methods and Fourier transform infrared spectroscopy is highlighted. The study utilizes ultra-high resolution electrospray ionization mass spectrometric and Fourier transform infrared spectroscopic data on biodegradable plastics bags for foodstuffs; high accuracy quantum chemical static methods, molecular dynamics; and chemometrics. There is achieved method performance |r| = 0.99981 determining poly(propylene glycol) in bag for foodstuff containing 20,416 species and using stochastic dynamics mass spectrometric formulas. The results highlight their great capability and applicability to the analytical science as well as relevance to both the fundamental research and to the industry.
The use of R code for modeling and simulation of 2-D contaminant migration through a soil for the pulse source
Vol 5, Issue 1, 2024
Download PDF
Abstract
In this study, based on an existing analytical solution for the two-dimensional transport of contaminants in a saturated soil layer, for the pulse source, the R program code was developed. The simulation is used to obtain the profiles of contaminant concentration, for a steady groundwater velocity, as a function of distance from the source and time. The problem is analytically solved by leveraging the similarity between the Gaussian (normal) distribution and contaminant concentration distribution, the development of the analytical model (i.e., solution of partial differential equation) by using this similarity is explained step by step since it may be of interest to researchers. Contaminant propagation is modeled using R software, which helps to understand how contaminants migrate through a saturated soil layer. This approach aids in comprehending the mechanisms and spatial dynamics of contaminant dispersion, facilitating the prediction and management of soil and groundwater contamination. The provided R code can be altered for different parameters and time intervals.
Keywords
References
- Bear J. Dynamics of Fluid in Porous Media. American Elsevier Publishing Company, New York; 1972.
- Freeze RA, Cherry JA. Groundwater, 2nd ed. Prentice Hall, Eaglewood, Cliff, New Jersey; 1979.
- Bear J, Verruijt A. Modeling Groundwater Flow and Pollution (Theory and Applications of Transport in Porous Media) D. Reidel Pub. Co., Holland; 1987.
- Rushton KR. Ground Water Hydrology Conceptual and Computational Models. John Wiley and Sons; 2003.
- Brenner A, Shacham M, Cutlip MB. Applications of the mathematical software packages for modeling and simulations in environmental engineering education, Environmental Modeling and Software. 2005; 20(10): 1307-1313.
- Bedient PB, Rifai HS, Newell CJ. Groundwater contamination transport and remediation. Prentice Hall; 1994.
- Cokca E. A computer program for the analysis of 1-D contaminant migration through a soil layer. Environmental Modelling & Software. 2003; 18: 147-153. doi: 10.1016/S1364-8152(02)00055-5
- Cokca E, Bilge T, Unutmaz B. Simulation of Contaminant Migration Through a Soil Layer Due to an Instantaneous Source. Computer Applications in Engineering Education. 2011; 19: 385-398. doi: 10.1002/cae.20320
- Cokca E, Aktas T. A course delivery method by using a software to predict contaminant migration through a soil layer. Computer Applications in Engineering Education. 2018; 26. doi: 10.1002/cae.22027
- Zheng C, Bennett GD. Applied Contaminant Transport Modeling. Wiley-Interscience; 2002.
- Ding XH, Feng SJ. Analytical model for degradable contaminant transport through cutoff wall-aquifer system under time-dependent point source pollution. Computers and Geotechnics. 2022; 143: 104627.
- Shu X, Wu Y, Zhang X, Yu F. Experiments and models for contaminant transport in unsaturated and saturated porous media—A Review. Chemical Engineering Research and Design. 2023; 192: 606-621.
- Soraganvi VS, Ababou R, Kumar MS. Effective flow and transport properties of heterogeneous unsaturated soils. Advances in Water Resources. 2020; 143.
- Zheng J, Yang Y, L J., et al. The migration mechanism of BTEX in single and double-lithology soil columns under groundwater table fluctuation. Toxics. 2023; 11. doi: 10.3390/toxics11070630
- Behdad A, Moradi M. Physical modelling of the voluminous spill and migration of LNAPL contaminants in unsaturated soil. Physical Modelling in Geotechnics, Korean Geotechnical Society (KGS); 2022. pp. 980-983.
- Rahhal J, Racha H, Muhsin E. Understanding soil contamination by leachate from landfills. In: Proceedings of the 9ICEG 9thInternational Congress on Environmental Geotechnics; 2023; Chania, Greece.
- Feo A, Celico F. Investigating the migration of immiscible contaminant fluid flow in homogeneous and heterogeneous aquifers with high-precision numerical simulations. PLoS ONE. 2022; 17(4): e0266486.
- Zhou J, Song B, Yu L, et al. Numerical research on migration law of typical chlorinated organic matter in shallow groundwater of Yangtze delta region. Water. 2023; 15: 1381.
- You X, Liu S, Dai C, et al. Contaminant occurrence and migration between high- and low-permeability zones in groundwater systems: A Review. Science of the Total Environment. 2020; 743: 140703.
- Filippini M, Parker BL, Dinelli E, et al. Assessing aquitard integrity in a complex aquifer aquitard system contaminated by chlorinated hydrocarbons. Water Research. 2020; 171: 115388.
- Chowdhury A, Rahnuma M. Groundwater contaminant transport modeling using MODFLOW and MT3DMS: a case study in Rajshahi City. Water Practice & Technology. 2023; 18(5): 1255. doi: 10.2166/wpt.2023.076
- Pareta K. Groundwater contamination modelling in Ayad River Basin. Udaipur, Scientific Reports. 2024; 14: 16624.
- Watts RJ. Hazardous waste: sources, pathways, receptors. Wiley, New York; 1998.
- De Long DJ. Longitudinal and Transverse Diffusion in Granular Deposits. Transactions American Geophysical Union; 1958. doi: 10.1029/TR039i001p00067
- R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria; 2021.
Supporting Agencies
Copyright (c) 2024 Atilla Onat Türkel, Erdal Çokça
License URL: https://creativecommons.org/licenses/by/4.0/

This site is licensed under a Creative Commons Attribution 4.0 International License (CC BY 4.0).
.jpg)
Beijing University of Technology, China



