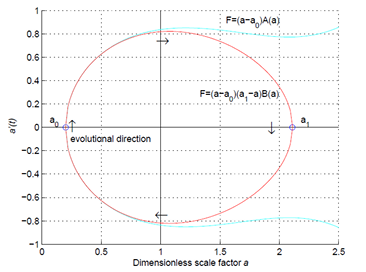
The present paper treats mainly two questions, namely the mathematical characterization of the notion of biodiversity of a border interface between two adjacent ecosystems, and the role of human interference in the physical reality of interacting multi-species systems. Mathematically, the techniques of reaction-diffusion modeling, Turing’s notion of flow matrices and Verhulst logistic growth dynamics are introduced, in order to model the complex interactions in a fractal, non-stationary ecosystem. A new key approach is the combined use of flow matrices and Verhulst growth dynamics with Laplace transforms. However, these findings so far remain theoretical, not in the least because of the widespread interference of human activities with ecological developments, both planned and unplanned. When comparing mathematical models and the actual physical dynamics of ecosystems, parallel trends as well as species-specific, unique deviations are conspicuous. Especially the latter remain hard to predict, indicating the limited value of mathematical predictions for the actual biodiversity trends in the field. Moreover, in a specific case study from the Netherlands related to the ecology of game mammals and a top-predator (the Wolf), it appears that not only contemporary ecological management operations, but also the contingency of measures from a historical past (exceeding 200 years) play a significant role in understanding the human interference factor in nature (designated as the Anthropocene factor).

1.         Hallmann CA, Sorg M, Jongejans E, et al. More than 75 percent decline over 27 years in total flying insect biomass in protected areas. PLOS ONE. 2017; 12(10): e0185809. doi: 10.1371/journal.pone.0185809

2.         Piatt JF, Parrish JK, Renner HM, et al. Extreme mortality and reproductive failure of common murres resulting from the northeast Pacific marine heatwave of 2014–2016. PLOS ONE. 2020; 15(1): e0226087. doi: 10.1371/journal.pone.0226087

3.         Weston P. ‘The scale is hard to grasp’: Avian flu wreaks devastation on seabirds. Earth Island Journal. 2022.

4.         Allen AR, Skuce RA, Byrne AW. Bovine tuberculosis in Britain and Ireland—A perfect storm? The confluence of potential ecological and epidemiological impediments to controlling a chronic infectious disease. Frontiers in Veterinary Science. 2018; 5. doi: 10.3389/fvets.2018.00109

5.         Animal & Plant Health Agency (Department for Environment, Food & Rural Affairs). Updated outbreak assessment for bluetongue virus in Europe (updated September 11, 2024). Available online: https://www.gov.uk/government/publications/bluetongue-virus-in-europe (accessed on 8 March 2025).

6.         Freedman HI. Deterministic Mathematical Models in Population Ecology. New York: Marcel Dekker; 1980.

7.         Addicott JF. Stability properties of 2-species models of mutualism: Simulation studies. Oecologia. 1981; 49(1): 42–49. doi: 10.1007/bf00376896

8.         Rai B, Freedman HI, Addicott JF. Analysis of three species models of mutualism in predator-prey and competitive systems. Mathematical Biosciences. 1983; 65(1): 13–50. doi: 10.1016/0025-5564(83)90069-X

9.         Krikorian N. The volterra model for three species predator-prey systems: Boundedness and stability. Journal of Mathematical Biology. 1979; 7(2): 117–132. doi: 10.1007/bf00276925

10.      Hsu SB, Ruan S, Yang TH. Analysis of three species Lotka-Volterra food web models with omnivory. Journal of Mathematical Analysis and Applications. 2015; 426(2): 659–687. doi: 10.1016/j.jmaa.2015.01.035

11.      Allaerts W. Stochastic reaction-diffusion modeling and epidemiology in a post-COVID-19 era. Austin Journal of Public Health and Epidemiology. 2021; 8(5): 1112.

12.      Renshaw E. Stochastic effects in population models. In: McGlade J (editor). Advanced Ecological Theory: Principles and Applications. London: Blackwell Science; 1999. pp. 23–63.

13.      Volterra V. Variations in the number of individuals in coexisting animal species (Italian). In: Animal Ecology. New York: McGraw Hill; 1926. pp. 409–448.

14.      Allaerts W. Towards a time-integrated convolution of the fractal biodiversity interface: The relation between biodiversity and entropy re-examined. Advances in Earth Science. 2025; 6(3): 1–9. doi: 10.47485/2766-2624.1071

15.      Allaerts W. Life as a dissipative structure. A metabletic exploration of public health research. Communication & Cognition. 2024; 57(1-2): 105–126. doi: 10.57028/c57-105-z1060

16.      Law R. Theoretical aspects of community assembly. In: McGlade J (editor). Advanced Ecological Theory: Principles and Applications. London: Blackwell Science; 1999. pp. 143–171.

17.      Golubitsky M, Stewart I. The symmetry perspective. From equilibrium to chaos in phase space and physical space. Basel, Boston, Berlin: Birkhäuser Verlag; 2002.

18.      Lyapunov AM. The General Problem of the Stability of Motion (Russian) [PhD thesis]. Kharkov University; 1966.

19.      Goh BS. Global Stability in Many-Species Systems. The American Naturalist. 1977; 111(977): 135–143. doi: 10.1086/283144

20.      Allaerts W. Evaluating the connectivity, continuity and distance norm in mathematical models for community ecology, epidemiology and multicellular pathway prediction. Journal of Physics: Conference Series. 2019; 1391(1): 012119. doi: 10.1088/1742-6596/1391/1/012119

21.      Hengeveld R. Von Uexküll’s Umwelt Concept Revived. Acta Biotheoretica. 2024; 72(4). doi: 10.1007/s10441-024-09487-9

22.      Hengeveld R. Dynamic Biogeography. Cambridge: Cambridge University Press; 1990.

23.      Carslaw HS, Jaeger JC. Conduction of Heat in Solids. Oxford: Clarendon Press; 1959. p. 29.

24.      Allaerts W. The unified neutral theory of biodiversity and biogeography revisited. Advances in Earth and Environmental Science. 2023; 4(2): 1–10.

25.      Allaerts W, Wouters A, van der Massen D, et al. A diffusion-adsorption model for the computation of the amount of hormone around a secreting cell, detected by the Reverse Hemolytic Plaque Assay. Journal of Theoretical Biology. 1988; 131: 441–459.

26.      Youssri YH, Atta AG. Petrov-Galerkin Lucas polynomials procedure for the time-fractional diffusion equation. Contemporary Mathematics. 2023; 4(2): 230–248. doi: 10.37256/cm.4220232420

27.      Janis CM, Carrano M. Scaling of reproductive turnover in archosaurs and mammals: why are terrestrial mammals so rare? Annales Zoologici Fennici. 1992; 28: 201–216.

28.      Werner J, Griebeler EM. Reproductive Biology and Its Impact on Body Size: Comparative Analysis of Mammalian, Avian and Dinosaurian Reproduction. PLoS ONE. 2011; 6(12): e28442. doi: 10.1371/journal.pone.0028442

29.      Metz AAJ, Diekmann O. The Dynamics of Physiologically Structured Populations. New York: Springer Verlag; 1986.

30.      Murray JD. Mathematical Biology. Berlin, Heidelberg: Springer Verlag; 1989.

31.      Brinkmann HW, Klotz EA. Linear Algebra and Analytic Geometry. Addison-Wesley Educational Pub; 1971.

32.      Turing AM. Morphogen theory of phyllotaxis. In: Saunders PT (editor). Collected Works of A.M. Turing. Part3. Morphogenesis. Amsterdam, London, New York: North-Holland (Elsevier Science Publishers BV); 1953. pp. 69–88.

33.      Bravais L, Bravais A. Essay on the arrangement of curviserial leaves (French). Annales Science Naturelle Botanique. 1837; (2): 42,193.

34.      Allaerts W. Fifty years after Alan M. Turing: An extraordinary theory of morphogenesis. Belgian Journal of Zoology. 2003; 133(1): 3–14.

35.      Allaerts W. Turing’s apple. Or the emergence of a modern myth (Dutch). bi-logical. 2008; 1(1): 10–25.

36.      Williams J. Laplace transforms. Series: Problem Solvers. London: George Allen & Unwin Ltd; 1973.

37.      Verhulst PF. Notice on the law that the population pursues in its increase (French). Correspondance Mathématique et Physique. 1838; 10: 113–121.

38.      Allaerts W. On land use and biodiversity resilience: Hydrology, temperature regulation and the fractal nature of the woodland-grassland interface. Austin Environmental Sciences. 2023; 8(2). doi: 10.26420/austinenvironsci.2023.1097

39.      Allaerts W. Estimating biodiversity and the fractal nature of ecosystems. International Journal of Bioinformatics and Computational Biology. 2020; 5(1): 15–24.

40.      Sheldrake R. A new science of life: The hypothesis of formative causation. London: Blond and Briggs; 1981.

41.      Maddox J. A book for burning? Nature. 1981; 293: 245–246. doi: 10.1038/293245b0

42.      Kayzer W, Sacks O, Gould SJ, et al. A Wonderful Accident (Dutch). Amsterdam, Antwerpen: Uitgeverij Contact; 1995.

43.      de Broglie LV. On the Theory of Quanta [PhD thesis]. Foundation of Louis de Broglie; 1924.

44.      Allaerts W. Inquiry into the spatio-temporal contingency of cellular communication systems. Communication & Cognition. 1992; 25(4): 277–294.

45.      Gardner M. Knotted Doughnuts and other Mathematical Entertainments. New York: W.H. Freeman and Company; 1986. pp. 205–221.

46.      Odds FC. Spirolaterals. The Mathematics Teacher. 1973; 66(2): 121–124. doi: 10.5951/mt.66.2.0121

47.      Beeler M. Paterson’s Worm: Artificial Intelligence Memo No. 290. Cambridge, MA: Massachusetts Institute of Technology; 1973.

48.      Peterson RT, Mountfort G, Hollom PAD. A field guide to the birds of Britain and Europe. In: Kist J, Van Oordt GJ (translation). Vogelgids. Amsterdam, Brussel: Elsevier; 1962.

49.      SOVON. Northern Raven. Distribution and trends (Dutch) (data 1990–2025). Stichting Vogelonderzoek Nederland (SOVON). Available online: https://stats.sovon.nl/stats/soort/15720 (accessed on 21 January 2025).

50.      Gravendeel B, de Groot A, Kik M, et al. The first wolf found in the Netherlands in 150 years was the victim of a wildlife crime. Lutra. 2013; 56(2): 93–109.

51.      Bij12. Verspreiding Wolf in Nederland (Dutch). Available online: https://www.bij12.nl/onderwerp/wolf/verspreiding-wolf-in-nederland/ (accessed on 21 January 2025).

52.      Broekhuizen S, Hoekstra B, van Laar V, et al. Atlas of the Dutch Mammals (Dutch). Schoorl: Uitgeverij Pirola; 1992. pp. 197–207.

53.      Brouwer GA. (1949). Some historical details about the red deer in the Netherlands and a reflection on the Veluwe deer as a nature conservation object (Dutch). In: In het voetspoor van Thijsse: Een reeks bijdragen over veldbiologie, natuurbescherming en landschap. Wageningen: H. Veenman & Zonen; 1949. pp. 214–247.

54.      National Park Service. Yellowstone wolf project 2023. Available online: https://www.nps.gov/yell/learn/nature/upload/2023-Wolf-Report-final_web.pdf (accessed on 21 January 2025).

55.      British Trust for Ornithology (BTO). Garden Birdwatch: Trichomonosis. Available online: https://www.bto.org (accessed on 21 January 2025).

56.      Dutch Wildlife Health Center. Trichomonas sp. infection in a Greenfinch. Available online: https://www.dwhc.nl (accessed on 21 January 2025).

57.      Morton T. Hyperobjects: Philosophy and Ecology After the End of the World. Minneapolis: University of Minnesota Press; 2013.