
Why the big bang never happened
Vol 2, Issue 2, 2024
Download PDF
Abstract
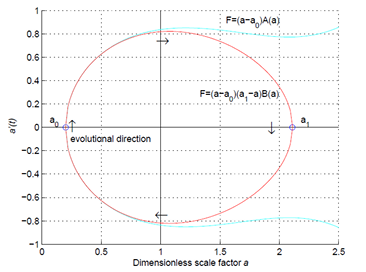
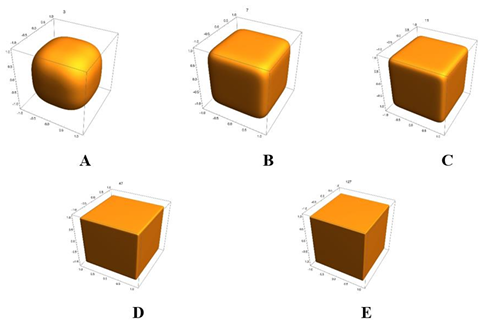
If general relativity is correct, then the origin of the universe is a simple mathematical problem. The Friedmann equation in cosmology is a well-structured ordinary differential equation, and the global properties of its solutions can be qualitatively analyzed by the phase-trajectory method. In this paper we show that the total energy density of matter in the universe is positive, and the total pressure near the Big Bang is negative. By analyzing the global properties of the solutions to the Friedmann equation according to these two conditions of state functions, we find that the Big Bang is impossible, and the space must be a closed 3-dimensional sphere, the cosmological constant is likely to be zero, and the evolution of the universe should be cyclic. The analysis and the proof are simple and straight forward, therefore these conclusions should be reliable.
Keywords
References
- Weinberg S. Gravitation and Cosmology. New York: Wiley; 1972.
- Gu YQ. Dynamical Reason for a Cyclic Universe. Symmetry. 2021; 13(12): 2272. doi: 10.3390/sym13122272
- Caldwell RR, Dave R, Steinhardt PJ. Cosmological Imprint of an Energy Component with General Equation of State. Physical Review Letters. 1998; 80(8): 1582–1585. doi: 10.1103/physrevlett.80.1582
- Turner MS. Dark Matter and Dark Energy in the Universe. Physica Scripta. 2000; T85(1): 210. doi: 10.1238/physica.topical.085a00210
- Peebles PJE, Ratra B. The cosmological constant and dark energy. Reviews of Modern Physics. 2003; 75(2): 559–606. doi: 10.1103/revmodphys.75.559
- Carroll SM. Quintessence and the Rest of the World: Suppressing Long-Range Interactions. Physical Review Letters. 1998; 81: 3067. doi: 10.1103/PhysRevLett.81.3067
- Zlatev I, Wang LM, Steinhardt PJ. Quintessence, Cosmic Coincidence, and the Cosmological Constant. Physical Review Letters. 1999; 82: 896-899. doi: 10.1103/PhysRevLett.82.896
- Faraoni V. Inflation and quintessence with nonminimal coupling. Physical Review D. 2000; 62: 023504. doi:10.1103/PhysRevD.62.023504
- Gasperini M, Piazza F, Veneziano G. Quintessence as a runaway dilaton. Physical Review D. 2002; 65: 023508. doi: 10.1103/PhysRevD.65.023508
- Capozziello S. Curvature Quintessence. International Journal of Modern Physics D. 2002; 11: 483. doi: 10.1142/S0218271802002025
- Caldwell RR, Linder EV. Limits of Quintessence. Physical Review letter. 2005; 95: 141301. doi: 10.1103/PhysRevLett.95.141301
- Astashenok AV, Nojiri S, Odintsov SD, Scherrer RJ. Scalar dark energy models mimicking ΛCDM with arbitrary future evolution. Physics Letters B. 2012; 713: 145-153. doi: 10.1016/j.physletb.2012.06.017
- Tsujikawa S. Quintessence: A review. Quantum Gravity. 2013; 30: 214003. doi: 10.1088/0264-9381/30/21/214003
- Shahalam M, Pathak SD, Verma MM, et al. Dynamics of interacting quintessence. The European Physical Journal C. 2015; 75(8): 395. doi: 10.1140/epjc/s10052-015-3608-1
- Han C, Pi S, Sasaki M. Quintessence saves Higgs instability. Physics Letters B. 2019; 791: 314-318. doi: 10.1016/j.physletb.2019.02.037
- Sahni V. The cosmological constant problem and quintessence. Classical and Quantum Gravity. 2002; 19(13): 3435–3448. doi: 10.1088/0264-9381/19/13/304
- S. Turner M, Huterer D. Cosmic Acceleration, Dark Energy, and Fundamental Physics. Journal of the Physical Society of Japan. 2007; 76(11): 111015. doi: 10.1143/jpsj.76.111015
- Ishak M. Remarks on the Formulation of the Cosmological Constant/Dark Energy Problems. Foundations of Physics. 2007; 37(10): 1470–1498. doi: 10.1007/s10701-007-9175-z
- Szydłowski M, Kurek A, Krawiec A. Top ten accelerating cosmological models. Physics Letters B. 2006; 642(3): 171–178. doi: 10.1016/j.physletb.2006.09.052
- Szydłowski M. Cosmological Zoo—accelerating models with dark energy. Journal of Cosmology and Astroparticle Physics. 2007; 2007(09): 007–007. doi: 10.1088/1475-7516/2007/09/007
- Copeland EJ, Sami M, Tsujikawa S. Dynamics of Dark Energy. International Journal of Modern Physics D. 2006; 15(11): 1753–1935. doi: 10.1142/s021827180600942x
- Linder EV. Theory challenges of the accelerating Universe. Journal of Physics A: Mathematical and Theoretical. 2007; 40(25): 6697–6705. doi: 10.1088/1751-8113/40/25/s14
- Bull P, Akrami Y, Adamek J, et al. Beyond ΛCDM: Problems, solutions, and the road ahead. Physics of the Dark Universe. 2016; 12: 56–99. doi: 10.1016/j.dark.2016.02.001
- Steinhardt PJ, Turok N. A Cyclic Model of the Universe. Science. 2002; 296(5572): 1436–1439. doi: 10.1126/science.1070462
- Barrow JD, Kimberly D, Magueijo J. Bouncing universes with varying constants. Classical and Quantum Gravity. 2004; 21(18): 4289–4296. doi: 10.1088/0264-9381/21/18/001
- Novello M, Bergliaffa S. Bouncing cosmologies. Physics Reports. 2008; 463(4): 127–213. doi: 10.1016/j.physrep.2008.04.006
- Liu L, Jiang Y, Qian Z. The Inflationary Universe Scenario. In: 10–35 Sec. after the Big Bang. Progress in Physics. 1989; 9(2): 121–187.
- Gu YQ. Clifford Algebra, Lorentz Transformation and Unified Field Theory. Advances in Applied Clifford Algebras. 2018; 28(2). doi: 10.1007/s00006-018-0852-0
- Gu YQ. Structure of the Star with Ideal Gases. Journal of High Energy Physics, Gravitation and Cosmology. 2022; 08(01): 100–114. doi: 10.4236/jhepgc.2022.81008
- Rong-Gen C, Li-Ming C, Li L, et al. Spacetime singularities and cosmic censorship conjectures. SCIENTIA SINICA Physica, Mechanica & Astronomica. 2022; 52(11): 110401. doi: 10.1360/sspma-2022-0069
- Gu YQ. Natural Coordinate System in Curved Space-Time. Journal of Geometry and Symmetry in Physics. 2018; 47: 51–62. doi: 10.7546/jgsp-47-2018-51-62
Supporting Agencies
Copyright (c) 2024 Yingqiu Gu
License URL: https://creativecommons.org/licenses/by/4.0/
Editor-in-Chief

Prof. Youssri Hassan Youssri
Cairo University, Egypt
Asia Pacific Academy of Science Pte. Ltd. (APACSCI) specializes in international journal publishing. APACSCI adopts the open access publishing model and provides an important communication bridge for academic groups whose interest fields include engineering, technology, medicine, computer, mathematics, agriculture and forestry, and environment.


.jpg)

.jpg)
