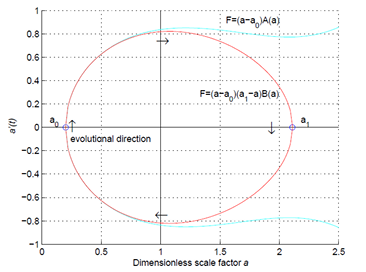
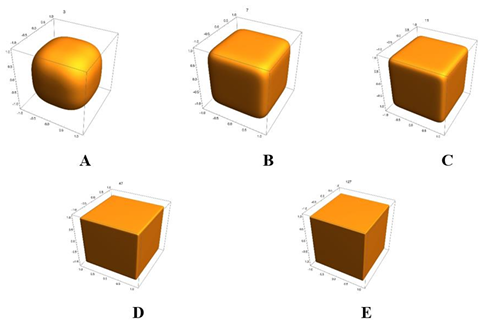
Fermat surfaces and hypercubes
Vol 2, Issue 1, 2024
Issue release: 30 June 2024
VIEWS - 699 (Abstract)
Download PDF
Abstract
Fermat’s last theorem appears not as a unique property of natural numbers but as the bottom line of extended possible issues involving larger dimensions and powers when observed from a natural vector space viewpoint. The fabric of this general Fermat’s theorem structure consists of a well-defined set of vectors associated with dimensional vector spaces and the Minkowski norms one can define there. Here, a special vector set is studied and named a Fermat surface. Besides, a connection between Fermat surfaces and hypercubes is unveiled.
Keywords
References
1. Wiles A. Modular Elliptic Curves and Fermat’s Last Theorem. The Annals of Mathematics. 1995; 141(3): 443. doi: 10.2307/2118559
2. Ossicini A. On the Nature of Some Euler’s Double Equations Equivalent to Fermat’s Last Theorem. Mathematics. 2022; 10(23): 4471. doi: 10.3390/math10234471
3. Klykov SP. Elementary proofs for the Fermat’s last theorem in Z using one trick for a restriction in ZP. Journal of Science and Arts. 2023; 23(3): 603-608. doi: 10.46939/j.sci.arts-23.3-a03
4. Klykov SP, Klykova MV. An elementary proof of Fermat’s last theorem. 2023. doi: 10.13140/RG.2.2.19455.59044
5. Gilbert JB. A Proof of Fermat’s Last Theorem. 2023. doi: 10.13140/RG.2.2.27051.82722
6. Castro C. Finding Rational Points of Circles, Spheres, Hyper-Spheres via Stereographic Projection and Quantum Mechanics. 2023. doi: 10.13140/RG.2.2.12030.36164
7. Carbó-Dorca R. Natural Vector Spaces (inward power and Minkowski norm of a Natural Vector, Natural Boolean Hypercubes) and a Fermat’s Last Theorem conjecture. Journal of Mathematical Chemistry. 2016; 55(4): 914-940. doi: 10.1007/s10910-016-0708-6
8. Carbó-Dorca R, Muñoz-Caro C, Niño A, et al. Refinement of a generalized Fermat’s last theorem conjecture in natural vector spaces. Journal of Mathematical Chemistry. 2017; 55(9): 1869-1877. doi: 10.1007/s10910-017-0766-4
9. Niño A, Reyes S, Carbó-Dorca R. An HPC hybrid parallel approach to the experimental analysis of Fermat’s theorem extension to arbitrary dimensions on heterogeneous computer systems. The Journal of Supercomputing. 2021; 77(10): 11328-11352. doi: 10.1007/s11227-021-03727-2
10. Carbó-Dorca R, Reyes S, Niño A. Extension of Fermat’s last theorem in Minkowski natural spaces. Journal of Mathematical Chemistry. 2021; 59(8): 1851-1863. doi: 10.1007/s10910-021-01267-x
11. Carbó-Dorca R. Whole Perfect Vectors and Fermat’s Last Theorem. Journal of Applied Mathematics and Physics. 2024; 12(01): 34-42. doi: 10.4236/jamp.2024.121004
12. Carbó-Dorca R. Rational Points on Fermat’s Surfaces in Minkowski’s (N+1) -Dimensional Spaces and Extended Fermat’s Last Theorem: Mathematical Framework and Computational Results. Unpublished Preprint. 2023. doi: 10.13140/RG.2.2.34181.52967
13. Carbó-Dorca R. Boolean hypercubes and the structure of vector spaces. Journal of Mathematical Sciences and Modelling. 2018; 1(1): 1-14. doi: 10.33187/jmsm.413116
14. Carbó-Dorca R. Fuzzy sets and Boolean tagged sets, vector semispaces and convex sets, QSM and ASA density functions, diagonal vector spaces and quantum Chemistry. Adv. Molec. Simil. 1998; 2: 43-72. doi: 10.1016/S1873-9776(98)80008-4
15. Carbó-Dorca R. Role of the structure of Boolean hypercubes when used as vectors in natural (Boolean) vector semispaces. Journal of Mathematical Chemistry. 2019; 57(3): 697-700. doi: 10.1007/s10910-018-00997-9
16. Carbó-Dorca R. Shadows’ hypercube, vector spaces, and non-linear optimization of QSPR procedures. Journal of Mathematical Chemistry. 2021; 60(2): 283-310. doi: 10.1007/s10910-021-01301-y
17. Carbó-Dorca R. Shell partition and metric semispaces: Minkowski norms, root scalar products, distances and cosines of arbitrary order. J. Math. Chem. 2002; 32: 201-223.
18. Bultinck P, Carbó-Dorca R. A mathematical discussion on density and shape functions, vector semispaces and related questions. J. Math. Chem. 2004; 36: 191-200. doi: 10.1023/B:JOMC.0000038793.21806.65
19. Carbó-Dorca R. Molecular quantum similarity measures in Minkowski metric vector semispaces. Journal of Mathematical Chemistry. 2008; 44(3): 628-636. doi: 10.1007/s10910-008-9442-z
20. Carbó-Dorca R, Chakraborty T. Extended Minkowski spaces, zero norms, and Minkowski hypersurfaces. Journal of Mathematical Chemistry. 2021; 59(8): 1875-1879. doi: 10.1007/s10910-021-01266-y
21. Carbó-Dorca R. Generalized scalar products in Minkowski metric spaces. Journal of Mathematical Chemistry. 2021; 59(4): 1029-1045. doi: 10.1007/s10910-021-01229-3
Refbacks
- There are currently no refbacks.
Copyright (c) 2024 Ramon Carbó-Dorca, Debraj Nath
License URL: https://creativecommons.org/licenses/by/4.0/
Editor-in-Chief
Prof. Youssri Hassan Youssri
Cairo University, Egypt
Indexing & Archiving
.jpg)
.jpg)
Asia Pacific Academy of Science Pte. Ltd. (APACSCI) specializes in international journal publishing. APACSCI adopts the open access publishing model and provides an important communication bridge for academic groups whose interest fields include engineering, technology, medicine, computer, mathematics, agriculture and forestry, and environment.