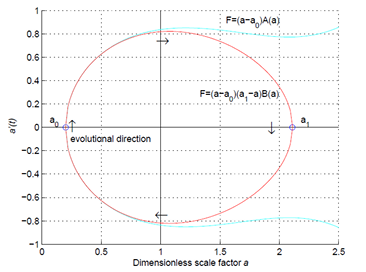
Correlating critical current density, quench protection, relaxation time and entropy in superconductors after disturbances—Intermediate summary
Vol 2, Issue 1, 2024
Issue release: 30 June 2024
VIEWS - 662 (Abstract)
Download PDF
Abstract
This paper summarizes results recently obtained from simulation of transient temperature excursions in filamentary and thin film superconductors. Under multi-component heat transfer in the complicated conductor cross sections and materials composition of present High Temperature Superconductors, numerical, Finite Element and Monte Carlo simulations are applied to solve Fourier’s differential equation with high spatial and temporal resolution. The overall aim was to encircle the quench problem in superconductors and to provide new stability criteria from correlations between superconductor critical current density, density of electron pairs, and relaxation time and entropy. Relaxation, correlation and entropy analysis presented in this paper extends the spectrum of standard methods to avoid quench to a new tool. As results, quench starts always locally, and as a highlight of this investigation, a second “critical” temperature, TQuench, has been identified that with high probability exists below standard critical temperature. Entropy is the driving force for relaxation of the superconductor to new equilibrium after a disturbance.
Keywords
References
1. Huebener RP. Magnetic Flux Structures in Superconductors. Springer Berlin Heidelberg; 1979. doi: 10.1007/978-3-662-02305-1
2. Kadin AM. Spatial Structure of the Cooper Pair. Journal of Superconductivity and Novel Magnetism. 2007; 20(4): 285-292. doi: 10.1007/s10948-006-0198-z
3. Wilson MN. Superconducting magnets. In: Scurlock RG (editor). Monographs on cryogenics. Oxford University Press; 1989.
4. Dresner L. Stability of superconductors. In: Wolf St (editor). Selected topics in superconductivity. Plenum Press; 1995.
5. Cardwell DA, Larbalestier DC, Braginski AI. Handbook of Superconductivity. CRC Press; 2022. doi: 10.1201/9781003139638
6. Reiss H. Finite Element Simulation of Temperature and Current Distribution in a Superconductor, and a Cell Model for Flux Flow Resistivity—Interim Results. Journal of Superconductivity and Novel Magnetism. 2016; 29(6): 1405-1422. doi: 10.1007/s10948-016-3492-4
7. Reiss H. Inhomogeneous Temperature Fields, Current Distribution, Stability and Heat Transfer in Superconductor 1G Multi-filaments. Journal of Superconductivity and Novel Magnetism. 2016; 29(6): 1449-1465. doi: 10.1007/s10948-016-3418-1
8. Reiss H. Stability of a (2G) Coated, Thin-Film YBaCuO 123 Superconductor: Intermediate Summary. Journal of Superconductivity and Novel Magnetism. 2020; 33(11): 3279-3311. doi: 10.1007/s10948-020-05590-3
9. Reiss H. An attempt to improve understanding the physics behind superconductor phase transitions and stability. Cryogenics. 2022; 124: 103325. doi: 10.1016/j.cryogenics.2021.103325
10. Buckel W, Kleiner R. Superconductivity. Published online January 2004. doi: 10.1002/9783527618507
11. Reiss H. A Microscopic Model of Superconductor Stability. Journal of Superconductivity and Novel Magnetism. 2012; 26(3): 593-617. doi: 10.1007/s10948-012-1800-1
12. Reiss H. Stability Considerations Using a Microscopic Stability Model Applied to a 2G Thin Film Coated Superconductor. Journal of Superconductivity and Novel Magnetism. 2017; 31(4): 959-979. doi: 10.1007/s10948-017-4245-8
13. Reiss H. Interpretation of experimental critical current density and levitation of superconductors, and a second temperature limit to protect superconductors against quench. ArXiv. 2023.
14. Annett J. Superconductivity, superfluids and condensates. Oxford University Press; 2004.
15. Flik ML, Tien CL. Intrinsic thermal stability of anisotropic thin- film superconductors. ASME Winter Ann. Meeting; 1988.
16. Falk G, Ruppel W. Energie und Entropie. Springer Berlin Heidelberg; 1976. doi: 10.1007/978-3-642-67899-8
17. Kreyszig E. Statistical methods and their applications (German). Vandenhoeck & Ruprecht; 1968.
18. Troitsky OYu, Reiss H. Estimation of thermal diffusivity of thin film materials by a one-level, two-point ’diverging’-thermal-wave technique. Part I: Theory. High Temperatures-High Pressures. 2003; 35/36(3): 265-280. doi: 10.1068/htjr100
19. Troitsky OYu, Reiss H. Flash Method for the Remote Sensing of the Thermal Diffusivity and the Absorption Coefficient at the Excitation Wavelength of Thin Film Materials. International Journal of Thermophysics. 2007; 28(5): 1536-1541. doi: 10.1007/s10765-007-0231-x
20. Troitsky OYu, Reiss H. A Numerical Simulation to Propose a Flash Method for In Situ Detection of the Thermal Diffusivity of Anisotropic Thin Film Materials. International Journal of Thermophysics. 2009; 30(4): 1283-1299. doi: 10.1007/s10765-009-0597-z
21. Reiss H, Troitsky OYu. Radiative transfer and its impact on thermal diffusivity determined in remote sensing. In: Reimer A (editor). Horizons in World Physics. Nova Science Publ. Inc; 2012.
22. Troitsky OYu, Reiss H. Radiative transfer and its impact on determination of thermal diffusivity in thin films. High Temperatures-High Pressures. 2017; 46: 313–341.
23. Agranat M, Ashitkov S, Kostanovskiĭ A, et al. Thermal radiation and electron - phonon relaxation produced by picosecond laser pulses in metals. High Temperatures-High Pressures. 1998; 30(6): 717-721. doi: 10.1068/htec91
24. Siegel R, Howell JR. Thermal Radiation Heat Transfer. McGraw- Hill Kogakusha Ltd.; 1972.
25. Parker WJ, Jenkins RJ. Thermal Conductivity Measurements on Bithmut Telluride in the Presence of a 2 MeV Electron Beam. Adv. Energy Conversion. 1962; 2: 87-103
26. Chandrasekhar S. Radiative transfer. Dover Publ., Inc.; 1960.
27. Whitaker St. Fundamental principles of heat transfer. Pergamon Press Inc; 1977
28. Carslaw HS, Jaeger JC. Conduction of Heat in Solids, 2nd ed. Oxford Science Publications, Clarendon Press; 1959.
29. Reiss H. The Additive Approximation for Heat Transfer and for Stability Calculations in a Multi-filamentary Superconductor. Journal of Superconductivity and Novel Magnetism. 2019.
30. Yuen WW, Wong LW. Heat Transfer by Conduction and Radiation in a One-Dimensional Absorbing, Emitting and Anisotropically-Scattering Medium. Journal of Heat Transfer. 1980; 102(2): 303-307. doi: 10.1115/1.3244278
31. Bohren CF, Huffmann DR. Absorption and scattering of light by small particles. Wiley- Interscience Publ.; 1983.
32. Fitzer G. Investigation of materials for the development of a superconducting switch (Germany). University of Karlsruhe; 1990.
33. Riise AB, Johansen TH, Bratsberg H, et al. Levitation force from high-Tcsuperconducting thin-film disks. Physical Review B. 1999; 60(13): 9855-9861. doi: 10.1103/physrevb.60.9855
34. Gray KE, Long AR, Adkins CJ. Measurements of the lifetime of excitations in superconducting aluminium. Philosophical Magazine. 1969; 20(164): 273-278. doi: 10.1080/14786436908228699
35. Gray KE. Steady state measurements of the quasiparticle lifetime in superconducting aluminium. Journal of Physics F: Metal Physics. 1971; 1(3): 290-308. doi: 10.1088/0305-4608/1/3/311
36. Mattuck RD. A guide to Feynman Diagrams in the many-body problem. MacGraw-Hill Book Company; 1967.
Refbacks
- There are currently no refbacks.
Copyright (c) 2024 Harald Reiss
License URL: https://creativecommons.org/licenses/by/4.0/
Editor-in-Chief
Prof. Youssri Hassan Youssri
Cairo University, Egypt
Processing Speed (2023)
-
-
- ＜7 days: submission to screening review decision
- 53 days: received to accepted
- 68 days: received to online
-
Asia Pacific Academy of Science Pte. Ltd. (APACSCI) specializes in international journal publishing. APACSCI adopts the open access publishing model and provides an important communication bridge for academic groups whose interest fields include engineering, technology, medicine, computer, mathematics, agriculture and forestry, and environment.